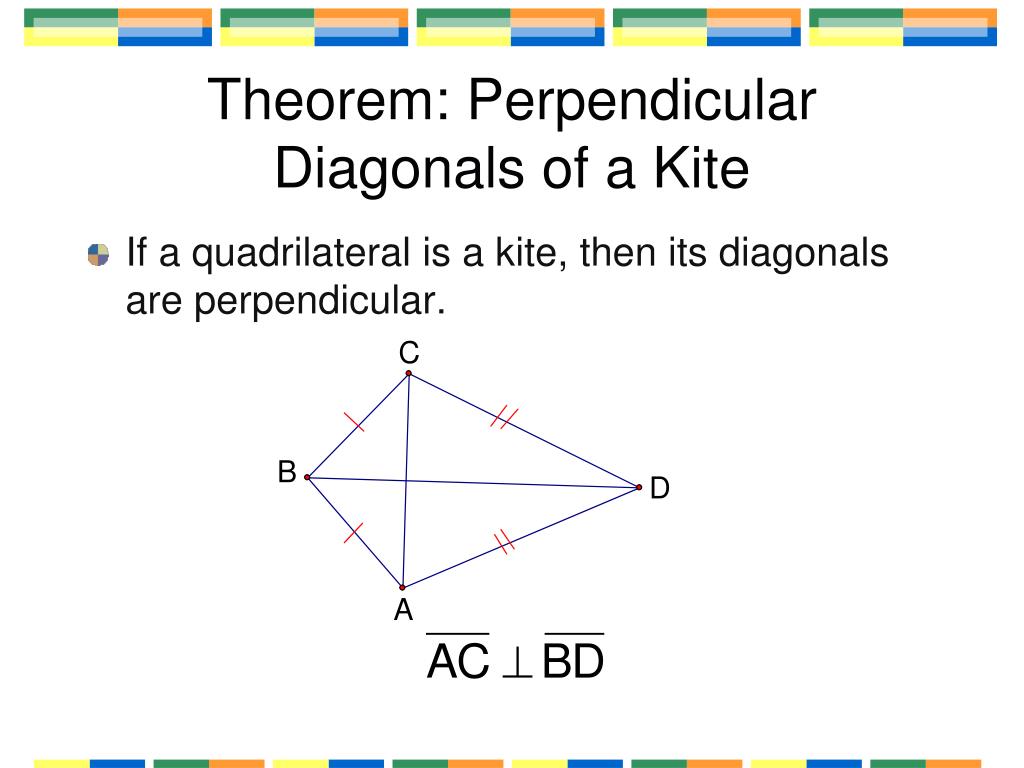
Kite Diagonals Are Perpendicular . Learn how to use triangle congruency and linear pair perpendicular theorem to show that the diagonals of a kite are. The area is one half the product of the diagonals. Let $abcd$ be a kite such that $ac$ and $bd$ are its diagonals. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; A kite can be a. (thus the kites are exactly the quadrilaterals that are both tangential and orthodiagonal.) the two line. Then $ac$ and $bd$ are perpendicular. D_2$ are lengths of diagonals. Perimeter of a kite with sides a and b is given. Here ac = longer diagonal and bd = shorter diagonal;
from www.slideserve.com
A kite can be a. Let $abcd$ be a kite such that $ac$ and $bd$ are its diagonals. D_2$ are lengths of diagonals. Here ac = longer diagonal and bd = shorter diagonal; The area is one half the product of the diagonals. Learn how to use triangle congruency and linear pair perpendicular theorem to show that the diagonals of a kite are. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. Then $ac$ and $bd$ are perpendicular. Perimeter of a kite with sides a and b is given.
PPT Trapezoids and Kites PowerPoint Presentation, free download ID
Kite Diagonals Are Perpendicular Perimeter of a kite with sides a and b is given. (thus the kites are exactly the quadrilaterals that are both tangential and orthodiagonal.) the two line. The area is one half the product of the diagonals. A kite can be a. Learn how to use triangle congruency and linear pair perpendicular theorem to show that the diagonals of a kite are. Here ac = longer diagonal and bd = shorter diagonal; The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; Perimeter of a kite with sides a and b is given. Let $abcd$ be a kite such that $ac$ and $bd$ are its diagonals. Then $ac$ and $bd$ are perpendicular. D_2$ are lengths of diagonals. Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle.
From slideplayer.com
Terms & Definitions Always, Sometimes Or Never Find the Measure Kite Diagonals Are Perpendicular (thus the kites are exactly the quadrilaterals that are both tangential and orthodiagonal.) the two line. D_2$ are lengths of diagonals. Then $ac$ and $bd$ are perpendicular. Let $abcd$ be a kite such that $ac$ and $bd$ are its diagonals. The area is one half the product of the diagonals. The two diagonals are perpendicular to each other with the. Kite Diagonals Are Perpendicular.
From www.cuemath.com
Area of a Kite Formula, Definition, Examples Kite Diagonals Are Perpendicular (thus the kites are exactly the quadrilaterals that are both tangential and orthodiagonal.) the two line. Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. The area is one half the product of the diagonals. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; A kite can be a.. Kite Diagonals Are Perpendicular.
From slideplayer.com
65 Trapezoids and Kites 2/15/17 ppt download Kite Diagonals Are Perpendicular Learn how to use triangle congruency and linear pair perpendicular theorem to show that the diagonals of a kite are. The area is one half the product of the diagonals. A kite can be a. D_2$ are lengths of diagonals. Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. Then $ac$ and. Kite Diagonals Are Perpendicular.
From db-excel.com
Proof The Diagonals Of A Kite Are Perpendicular — Kite Diagonals Are Perpendicular Here ac = longer diagonal and bd = shorter diagonal; Perimeter of a kite with sides a and b is given. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; Learn how to use triangle congruency and linear pair perpendicular theorem. Kite Diagonals Are Perpendicular.
From slideplayer.com
Objective To verify and use properties of trapezoids and kites. ppt Kite Diagonals Are Perpendicular The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; The area is one half the product of the diagonals. Then $ac$ and $bd$ are perpendicular. Perimeter of a kite with sides a and b is given. The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; A kite can be a.. Kite Diagonals Are Perpendicular.
From classfullrequotes.z21.web.core.windows.net
Finding The Area Of A Kite Kite Diagonals Are Perpendicular Then $ac$ and $bd$ are perpendicular. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; The area is one half the product of the diagonals. D_2$ are lengths of diagonals. Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. (thus the kites are exactly the quadrilaterals that are both. Kite Diagonals Are Perpendicular.
From slideplayer.com
65 Trapezoids and Kites 2/15/17 ppt download Kite Diagonals Are Perpendicular Here ac = longer diagonal and bd = shorter diagonal; The area is one half the product of the diagonals. Learn how to use triangle congruency and linear pair perpendicular theorem to show that the diagonals of a kite are. Then $ac$ and $bd$ are perpendicular. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Sal proves. Kite Diagonals Are Perpendicular.
From www.gauthmath.com
A kite has perpendicular diagonals with the measur Gauthmath Kite Diagonals Are Perpendicular A kite can be a. Then $ac$ and $bd$ are perpendicular. The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. Learn how to use triangle congruency and linear pair perpendicular theorem to show that the diagonals. Kite Diagonals Are Perpendicular.
From slideplayer.com
What are Kites? ppt download Kite Diagonals Are Perpendicular The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; Then $ac$ and $bd$ are perpendicular. Here ac = longer diagonal and bd = shorter diagonal; Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas. Kite Diagonals Are Perpendicular.
From www.ck12.org
Kites ( Read ) Geometry CK12 Foundation Kite Diagonals Are Perpendicular D_2$ are lengths of diagonals. Perimeter of a kite with sides a and b is given. Here ac = longer diagonal and bd = shorter diagonal; The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; The area is one half the product of the diagonals. Learn how to use triangle congruency and linear. Kite Diagonals Are Perpendicular.
From byjus.com
In which of the following quadrilaterals are the diagonals Kite Diagonals Are Perpendicular D_2$ are lengths of diagonals. Here ac = longer diagonal and bd = shorter diagonal; Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Perimeter of a kite with sides a and b is given. Then $ac$ and $bd$ are. Kite Diagonals Are Perpendicular.
From www.slideserve.com
PPT Trapezoids and Kites PowerPoint Presentation, free download ID Kite Diagonals Are Perpendicular D_2$ are lengths of diagonals. The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; Learn how to use triangle congruency and linear pair perpendicular theorem to show that the diagonals of a kite are. Perimeter of a kite with sides a and b is given. A kite can be a. The area of. Kite Diagonals Are Perpendicular.
From brainly.com
The diagonals of kite KITE intersect at point P. If m A. 34° B. 46° C Kite Diagonals Are Perpendicular (thus the kites are exactly the quadrilaterals that are both tangential and orthodiagonal.) the two line. The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. A kite can be a. The area of kite $= \frac{1}{2}. Kite Diagonals Are Perpendicular.
From slideplayer.com
G4.4 Trapezoids and Kites Objectives ppt download Kite Diagonals Are Perpendicular Here ac = longer diagonal and bd = shorter diagonal; The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Then $ac$ and $bd$ are perpendicular. Let $abcd$ be a kite such that $ac$ and $bd$ are its diagonals. The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; The area is. Kite Diagonals Are Perpendicular.
From www.scribd.com
Exploring the Properties of Kites Diagonals, Angles, and Area PDF Kite Diagonals Are Perpendicular Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. Here ac = longer diagonal and bd = shorter diagonal; The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; A kite can be a. Perimeter of a kite with sides a and b is given. (thus. Kite Diagonals Are Perpendicular.
From slideplayer.com
Section 6.5 Trapezoids and Kites. ppt download Kite Diagonals Are Perpendicular Here ac = longer diagonal and bd = shorter diagonal; Perimeter of a kite with sides a and b is given. Then $ac$ and $bd$ are perpendicular. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; Let $abcd$ be a kite. Kite Diagonals Are Perpendicular.
From www.varsitytutors.com
How to find the length of the diagonal of a kite ACT Math Kite Diagonals Are Perpendicular Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; The two diagonals are perpendicular to each other with the longer diagonal bisecting the shorter one; Learn how to use triangle congruency and linear pair perpendicular theorem to show that the. Kite Diagonals Are Perpendicular.
From firmfunda.com
Construction / Practical Geometry (basics) Perpendicular Bisector to Kite Diagonals Are Perpendicular Sal proves that the diagonals of a kite are perpendicular, by using the sss and sas triangle. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; A kite can be a. (thus the kites are exactly the quadrilaterals that are both tangential and orthodiagonal.) the two line. Perimeter of a kite with sides a and b is. Kite Diagonals Are Perpendicular.